Magische vierkanten
Een andere techniek om zelf sigils te maken, is om gebruik te maken van een magisch vierkant. Eerst even wat wiskundige uitleg over wat een magisch vierkant precies is. Iedereen die al wel eens een sudoku heeft ingevuld, weet eigenlijk al wat een magisch vierkant of tovervierkant is.
Een magisch vierkant is een vierkant van n bij n hokjes waarin de getallen van 1 tot en met n² zijn ingevuld, op zo’n manier dat minstens elke kolom en elke rij opgeteld dezelfde uitkomst geeft. n moet altijd groter zijn dan 2.
Het aantal rijen en kolommen wordt de orde n van het magisch vierkant genoemd. De som van een rij, kolom of diagonaal noemen we de magische constante, het karakteristiek getal of het tovergetal. Je kan de constante berekenenmet de volgende formule: 0,5 (n³+n)
We komen aan deze formule door de som te nemen van alle getallen van het tovervierkant: 1+2+...+(n²-1)+n². Dit is gelijk aan 0,5 n²(n² +1) . Delen door n levert dan som van de getallen van één rij of kolom.
Afgezien van het getal 1 (een vierkant van 1 bij 1 hokje) bestaat het eenvoudigste tovervierkant uit 3 op 3 cijfers (orde 3). De som van elke rij is dan 15. Een tovervierkant van orde 2 (met de cijfers 1 tot en met 4) is onmogelijk..
In de praktijk worden ook andere getallen gebruikt dan 1 tot en met n². Zo bestaan er tovervierkanten die alleen uit kwadraten of alleen uit priemgetallen bestaan. Die tovervierkanten zijn dus niet zuiver. Soms laat men zelfs de eis vallen dat de getallen verschillend moeten zijn, zodat ook een vierkant met 16 enen magisch genoemd wordt. Dat soort vierkanten wordt gebruikt bij de constructie van echte tovervierkanten.
Als niet alleen de rijen en kolommen maar ook de subdiagonalen dezelfde som opleveren, dan spreken we van een “pandiagonaal magisch vierkant” of een “panmagisch vierkant”.
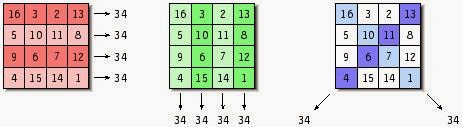
Bij een “perfect magisch vierkant” is in elk deelvierkant van orde 2 de som van de cijfers gelijk. In het voorbeeld hieronder is is niet alleen de som van elke rij, kolom en diagonaal 34, maar ook de som van elk van de negen mogelijke deelvierkanten van orde 2.
Magische vierkanten fascineren de mens al eeuwen. De geschiedenis van het magische vierkant gaat dan ook terug tot lang voor onze jaartelling. Je vindt ze in veel culturen overal ter wereld, zoals in Egypte, India, de Arabische wereld, enz. .... De oudste magische vierkanten die zijn gevonden dateren van meer dan 4.000 jaar geleden. Ze werden gegraveerd in steen of op metaal en gedragen als geluksbrenger.
Aan magische vierkanten worden magische krachten toegedicht. In het Chinese verhaal van Lo Shu wordt verteld over een enorme overstroming van de rivier Lo. De mythische Chinese keizer Yu had geprobeerd om een kanaal te graven naar de zee om zo het water af te voeren. Tijdens het graven werden er offers gebracht in de hoop de rivier gunstig te kunnen stemmen. Het offerritueel werd echter onderbroken door een schilpad die uit de rivier kwam gekropen, met op zijn schild een merkwaardig patroon van ronde stippen die in een rasterpatroon waren geplaatst van drie bij drie.
Tot zijn verbazing ontdekte de keizer dat de som van de stippen in elke rij, kolom en diagonaal 15 was. Voor de Chinezen was dit een bovennatuurlijk teken van orde en balans in het universum. 15 is het aantal dagen in elk van de 24 cycli van het Chinese zonnejaar. De Chinezen interpreteerden dit als een teken dat er 15 offers gebracht moesten worden, 1 voor iedere dag in de cyclus. Na de uitvoering van deze offergaven stopte de overstroming.
Dit meest elementaire tovervierkant werd Lo Shu of “kaart van de rivier” genoemd. Volgens de meer wetenschappelijke kanalen is het Loh Shu vierkant eigenlijk bedacht door de wiskundig geschoolde keizer Fuh-Hi, die gezien wordt als de grondlegger van de Chinese beschaving.
Lo Shu zou een belangrijke rol gaan spelen in het Chinese denken. Hij diende als inspiratiebron voor het bouwen van tempels, voor bewegingen in de tai chi, talismannen en Feng Shui. Loh Shu belichaamt het oosterse concept van Yin en Yang. De oneven getallen worden voorgesteld als witte punten die Yang symboliseren, de even getallen door zwarte punten die Yin voorstellen. Voor de Chinezen zijn de oneven getallen (Yang) het symbool van de hemel (het mannelijke) en de even getallen (Yin) het symbool voor de aarde (het vrouwelijke).
Het Lo Shu vierkant is een uniek magische vierkant van orde 3, met 1 aan de onderkant en 2 aan de rechterbovenhoek. Elk magische vierkant van orde 3 kan je uit het Lo Shu vierkant verkrijgen door het te draaien of te spiegelen. In astrologische kringen wordt het ook wel het Saturnusvierkant genoemd. De vrijmetselaars gebruiken dit vierkant als basis voor de numerieke codes waarmee ze hun loges aanduiden.
Het eerste magische vierkant van orde 4 duikt op in India omstreeks de 1ste eeuw en werd gemaakt door de wiskundige Nagarajuna. In Jaina geschriften uit de 12de eeuw is het eerste perfect magische vierkant gevonden. Jaina is een religie en filosofie maar het is niet bekend welke rol het magische vierkant in deze religie speelde.
De eerste vierkanten van de orde 5 en 6 zijn gevonden in Arabische geschriften van rond de 1ste eeuwwisseling. Waarschijnlijk hadden de Arabieren de kennis opgedaan van de Indiërs. De wiskundige Al- Buni werkte intensief met magische vierkanten en geloofde in de bovennatuurlijke eigenschappen ervan. Bronnen vermelden dat magische vierkanten werden gebruikt om astrologische berekeningen te maken en voorspellingen te doen.
Via de Arabieren bereikte de kennis over de magische vierkanten Europa. De Griek Manual Moschopoulos schrijft in 1300 echter alleen over de wiskundige eigenschappen. Pas anderhalve eeuw later worden de magische eigenschappen gedocumenteerd door de Italiaan Marsilio Ficino die medeoprichter was van een magische school. De meest gedetailleerde beschrijvingen over de magische eigenschappen van de vierkanten en hoe ze te construeren vinden we in het werk van Agrippa. Hij legt verbanden tussen de magische vierkanten en de planeetenergieën.
In de middeleeuwen al zochten magiërs en occultisten naar correspondenties die pasten bij de (toen) bekende 7 planeten: de Zon, Maan, Mercurius, Venus, Mars, Jupiter en Saturnus. De magische vierkanten werden als rekenkundige archetypes van de planeten beschouwd. De orde en de constante bepaalden onder welke invloed een bepaald magisch vierkant stond.
Wie de grondlegger is geweest van de toewijzing van getallen aan de planeten is onduidelijk. Veel bronnen verwijzen naar Agrippa, maar het kunnen ook de Arabieren of de Babyloniers zijn. De Babyloniers geloofden dat de aarde het middelpunt van de kosmos was waar de 7 planeten omheen draaiden, in deze volgorde: Maan, Mercurius, Venus, Zon, Mars, Jupiter, Saturnus. De planeet die het verst van de aarde verwijderd was kreeg het kleinste magische vierkant. Saturnus kreeg zo de orde 3 toegewezen, Jupiter orde 4, Mars orde 5, Zon orde 6, enz. ...
Het feit dat de Zon aan orde 6 gekoppeld is, is speciaal. Daardoor komt deze theorie immers overeen met een heel oud numerologisch systeem uit Soemerië. In deze cultuur werd de zon vereerd en zij hadden een zesvoudig telsysteem waarin werd vastgelegd dat de dag 24 uur duurde en de zon opkwam om 6u00 en onderging om 18u00. De Soemeriers waren ook de eersten om te stellen dat een cirkel uit 360 graden bestaat. Pythagoras noemde in zijn getallentheorie de 6 het eerste perfecte nummer. Het is te begrijpen dat het magische vierkant van orde 6 met een constante van 666 een diepe indruk maakte op de grondleggers van de westerse magie...
Elk van de 7 gekende planeten stond ook voor één van de sephirots of werelden op de Kabalistische wereldboom: Saturnus bijvoorbeeld is het planetair symbool voor Binah, de derde sephirot. Het magisch vierkant van Saturnus is dan ook een vierkant van orde 3. Hetzelfde geldt voor alle andere planeten.
Hoe kan je nu magische vierkanten gebruiken voor magisch werk? Je kan de magische vierkanten zelf gebruiken als één van de correspondenties voor de planeten. Zo kan je bijvoorbeeld een magisch vierkant van orde 7, dat staat voor de planeet Venus, gebruiken in een liefdesamulet.
Maar je kan magische vierkanten ook gebruiken om sigils te maken. In het onderstaande beeld zie je een amulet met het Saturnusvierkant (orde 3), het symbool voor Saturnus (linksboven) en de sigil van Saturnus (boven).
Die sigil kan je gemakkelijk uit het magisch vierkant van orde 3 halen. Verdeel de cijfers in het vierkant in groepen van 3. Groep 1 = 1 2 3, groep 2 = 4 5 6, groep 3 = 7 8 9. Trek nu lijnen tussen de cijfers van elke groep. Zo krijg je onderstaande tekening of sigil.
Zo kan je ook zelf sigils maken die je kan gebruiken voor runenmagie. De stappen blijven dezelfde, alleen maak je je rune nu niet door met letters te schuiven maar door een combinatie van numerologie en een magisch vierkant.
Nadat je je intentie hebt geformuleerd, zet je de letters die je overhoudt om in cijfers. Elke letter geef je het getal waarmee het overeenkomt. Bijvoorbeeld: A = 1, B = 2, enz. ... tot aan de letter Z = 26. Je kan hier andere numerologische verbanden leggen als je dat wil (veel numerologen werken tegenwoordig met fonetische verbanden in plaats van met het alfabet), maar dat is an sich niet belangrijk. Bepaalde letters komen overeen met een getal dat uit meer dan één cijfer bestaat. Die cijfers tel je op tot je een cijfer tussen 1 en 9 overhoudt.
In de westerse numerologie wordt soms ook wel met de volgende regel gewerkt:
1 = A / J / S
2 = B / K / T
3 = C / L / U
4 = D / M / V
5 = E / N / W
6 = F / O / X
7 = G / P / Y
8 = H / Q / Z
9 = I / R
Welke vorm van numerologie je ook gebruikt – de Hebreeuwse of Griekse geomatria, de Pythogoraanse numerologie, enz. ... – is helemaal niet belangrijk, als je maar consistent bent en steeds hetzelfde systeem gebruikt.
Herinner je de intentie die we eerder formuleerden:
Deze intentie werd omgezet in een letterwoord:
Dat letterwoord kunnen we numerologiegewijs omzetten in cijfers:
Verder vereenvoudigd wordt dit: 2-2-5-7-8-4-9-4-5-1-6-2-3-4
Kies vervolgens het magisch vierkant dat het beste past bij je intentie. Kijk daarvoor in de correspondentietabellen. Bijvoorbeeld: Saturnus staat voor wereldse dingen die met rijkdom te maken hebben, Venus staat voor liefdesgerelateerde intenties, enz. ... Weet je het niet zeker, gebruik dan het vierkant van Saturnus. Aangezien Saturnus verbonden is met onze materiële wereld, en we via onze runenmagie intenties willen gaan realiseren in die materiële wereld, is dat een passe-partout vierkant voor het maken van sigils.
Trek nu een lijn tussen de cijfers zodat je een symbool krijgt dat overeenkomt met je intentie. Zo heb je meteen een sigil gemaakt.
Om zelf magische vierkanten te maken, zijn er een aantal trukjes. Er is een methode voor vierkanten van een oneven orde en voor vierkanten van een even orde.
Magische vierkanten van een oneven orde:
Magische vierkanten van een even orde:
Vind je het te moeilijk om zelf de magische vierkanten uit te werken, dan vind je verschillende online berekeningsprograma’s op het internet die dat werkje van je overnemen (of je toelaten je eigen werk te controleren).
Werken met magische vierkanten en magische alfabetten heeft uiteindelijk tot doel om te communiceren met je onderbewustzijn (en met het collectieve onbewustzijn in de astraalwereld).
Ben je geïnteresseerd of zelfs gefascineerd door het tipje van de sluier dat hier werd opgelicht, ga dan op zoek naar informatie over de complexe methodieken van de ceremoniële magie en hoge magie. Vind je het allemaal echter veel te complex en te occult, hou het dan bij de simpele runenmagie en de correspondentietabellen. Het zou jammer zijn om het kind met het badwater weg te gooien en de hele runenmagie links te laten liggen. Deze vorm van magie is immers heel krachtig.
Een magisch vierkant is een vierkant van n bij n hokjes waarin de getallen van 1 tot en met n² zijn ingevuld, op zo’n manier dat minstens elke kolom en elke rij opgeteld dezelfde uitkomst geeft. n moet altijd groter zijn dan 2.
Het aantal rijen en kolommen wordt de orde n van het magisch vierkant genoemd. De som van een rij, kolom of diagonaal noemen we de magische constante, het karakteristiek getal of het tovergetal. Je kan de constante berekenenmet de volgende formule: 0,5 (n³+n)
We komen aan deze formule door de som te nemen van alle getallen van het tovervierkant: 1+2+...+(n²-1)+n². Dit is gelijk aan 0,5 n²(n² +1) . Delen door n levert dan som van de getallen van één rij of kolom.
Afgezien van het getal 1 (een vierkant van 1 bij 1 hokje) bestaat het eenvoudigste tovervierkant uit 3 op 3 cijfers (orde 3). De som van elke rij is dan 15. Een tovervierkant van orde 2 (met de cijfers 1 tot en met 4) is onmogelijk..
In de praktijk worden ook andere getallen gebruikt dan 1 tot en met n². Zo bestaan er tovervierkanten die alleen uit kwadraten of alleen uit priemgetallen bestaan. Die tovervierkanten zijn dus niet zuiver. Soms laat men zelfs de eis vallen dat de getallen verschillend moeten zijn, zodat ook een vierkant met 16 enen magisch genoemd wordt. Dat soort vierkanten wordt gebruikt bij de constructie van echte tovervierkanten.
Als niet alleen de rijen en kolommen maar ook de subdiagonalen dezelfde som opleveren, dan spreken we van een “pandiagonaal magisch vierkant” of een “panmagisch vierkant”.
Bij een “perfect magisch vierkant” is in elk deelvierkant van orde 2 de som van de cijfers gelijk. In het voorbeeld hieronder is is niet alleen de som van elke rij, kolom en diagonaal 34, maar ook de som van elk van de negen mogelijke deelvierkanten van orde 2.
Magische vierkanten fascineren de mens al eeuwen. De geschiedenis van het magische vierkant gaat dan ook terug tot lang voor onze jaartelling. Je vindt ze in veel culturen overal ter wereld, zoals in Egypte, India, de Arabische wereld, enz. .... De oudste magische vierkanten die zijn gevonden dateren van meer dan 4.000 jaar geleden. Ze werden gegraveerd in steen of op metaal en gedragen als geluksbrenger.
Aan magische vierkanten worden magische krachten toegedicht. In het Chinese verhaal van Lo Shu wordt verteld over een enorme overstroming van de rivier Lo. De mythische Chinese keizer Yu had geprobeerd om een kanaal te graven naar de zee om zo het water af te voeren. Tijdens het graven werden er offers gebracht in de hoop de rivier gunstig te kunnen stemmen. Het offerritueel werd echter onderbroken door een schilpad die uit de rivier kwam gekropen, met op zijn schild een merkwaardig patroon van ronde stippen die in een rasterpatroon waren geplaatst van drie bij drie.
Tot zijn verbazing ontdekte de keizer dat de som van de stippen in elke rij, kolom en diagonaal 15 was. Voor de Chinezen was dit een bovennatuurlijk teken van orde en balans in het universum. 15 is het aantal dagen in elk van de 24 cycli van het Chinese zonnejaar. De Chinezen interpreteerden dit als een teken dat er 15 offers gebracht moesten worden, 1 voor iedere dag in de cyclus. Na de uitvoering van deze offergaven stopte de overstroming.
Dit meest elementaire tovervierkant werd Lo Shu of “kaart van de rivier” genoemd. Volgens de meer wetenschappelijke kanalen is het Loh Shu vierkant eigenlijk bedacht door de wiskundig geschoolde keizer Fuh-Hi, die gezien wordt als de grondlegger van de Chinese beschaving.
Lo Shu zou een belangrijke rol gaan spelen in het Chinese denken. Hij diende als inspiratiebron voor het bouwen van tempels, voor bewegingen in de tai chi, talismannen en Feng Shui. Loh Shu belichaamt het oosterse concept van Yin en Yang. De oneven getallen worden voorgesteld als witte punten die Yang symboliseren, de even getallen door zwarte punten die Yin voorstellen. Voor de Chinezen zijn de oneven getallen (Yang) het symbool van de hemel (het mannelijke) en de even getallen (Yin) het symbool voor de aarde (het vrouwelijke).
Het Lo Shu vierkant is een uniek magische vierkant van orde 3, met 1 aan de onderkant en 2 aan de rechterbovenhoek. Elk magische vierkant van orde 3 kan je uit het Lo Shu vierkant verkrijgen door het te draaien of te spiegelen. In astrologische kringen wordt het ook wel het Saturnusvierkant genoemd. De vrijmetselaars gebruiken dit vierkant als basis voor de numerieke codes waarmee ze hun loges aanduiden.
Het eerste magische vierkant van orde 4 duikt op in India omstreeks de 1ste eeuw en werd gemaakt door de wiskundige Nagarajuna. In Jaina geschriften uit de 12de eeuw is het eerste perfect magische vierkant gevonden. Jaina is een religie en filosofie maar het is niet bekend welke rol het magische vierkant in deze religie speelde.
De eerste vierkanten van de orde 5 en 6 zijn gevonden in Arabische geschriften van rond de 1ste eeuwwisseling. Waarschijnlijk hadden de Arabieren de kennis opgedaan van de Indiërs. De wiskundige Al- Buni werkte intensief met magische vierkanten en geloofde in de bovennatuurlijke eigenschappen ervan. Bronnen vermelden dat magische vierkanten werden gebruikt om astrologische berekeningen te maken en voorspellingen te doen.
Via de Arabieren bereikte de kennis over de magische vierkanten Europa. De Griek Manual Moschopoulos schrijft in 1300 echter alleen over de wiskundige eigenschappen. Pas anderhalve eeuw later worden de magische eigenschappen gedocumenteerd door de Italiaan Marsilio Ficino die medeoprichter was van een magische school. De meest gedetailleerde beschrijvingen over de magische eigenschappen van de vierkanten en hoe ze te construeren vinden we in het werk van Agrippa. Hij legt verbanden tussen de magische vierkanten en de planeetenergieën.
In de middeleeuwen al zochten magiërs en occultisten naar correspondenties die pasten bij de (toen) bekende 7 planeten: de Zon, Maan, Mercurius, Venus, Mars, Jupiter en Saturnus. De magische vierkanten werden als rekenkundige archetypes van de planeten beschouwd. De orde en de constante bepaalden onder welke invloed een bepaald magisch vierkant stond.
Wie de grondlegger is geweest van de toewijzing van getallen aan de planeten is onduidelijk. Veel bronnen verwijzen naar Agrippa, maar het kunnen ook de Arabieren of de Babyloniers zijn. De Babyloniers geloofden dat de aarde het middelpunt van de kosmos was waar de 7 planeten omheen draaiden, in deze volgorde: Maan, Mercurius, Venus, Zon, Mars, Jupiter, Saturnus. De planeet die het verst van de aarde verwijderd was kreeg het kleinste magische vierkant. Saturnus kreeg zo de orde 3 toegewezen, Jupiter orde 4, Mars orde 5, Zon orde 6, enz. ...
Het feit dat de Zon aan orde 6 gekoppeld is, is speciaal. Daardoor komt deze theorie immers overeen met een heel oud numerologisch systeem uit Soemerië. In deze cultuur werd de zon vereerd en zij hadden een zesvoudig telsysteem waarin werd vastgelegd dat de dag 24 uur duurde en de zon opkwam om 6u00 en onderging om 18u00. De Soemeriers waren ook de eersten om te stellen dat een cirkel uit 360 graden bestaat. Pythagoras noemde in zijn getallentheorie de 6 het eerste perfecte nummer. Het is te begrijpen dat het magische vierkant van orde 6 met een constante van 666 een diepe indruk maakte op de grondleggers van de westerse magie...
Elk van de 7 gekende planeten stond ook voor één van de sephirots of werelden op de Kabalistische wereldboom: Saturnus bijvoorbeeld is het planetair symbool voor Binah, de derde sephirot. Het magisch vierkant van Saturnus is dan ook een vierkant van orde 3. Hetzelfde geldt voor alle andere planeten.
Hoe kan je nu magische vierkanten gebruiken voor magisch werk? Je kan de magische vierkanten zelf gebruiken als één van de correspondenties voor de planeten. Zo kan je bijvoorbeeld een magisch vierkant van orde 7, dat staat voor de planeet Venus, gebruiken in een liefdesamulet.
Maar je kan magische vierkanten ook gebruiken om sigils te maken. In het onderstaande beeld zie je een amulet met het Saturnusvierkant (orde 3), het symbool voor Saturnus (linksboven) en de sigil van Saturnus (boven).
Die sigil kan je gemakkelijk uit het magisch vierkant van orde 3 halen. Verdeel de cijfers in het vierkant in groepen van 3. Groep 1 = 1 2 3, groep 2 = 4 5 6, groep 3 = 7 8 9. Trek nu lijnen tussen de cijfers van elke groep. Zo krijg je onderstaande tekening of sigil.
Zo kan je ook zelf sigils maken die je kan gebruiken voor runenmagie. De stappen blijven dezelfde, alleen maak je je rune nu niet door met letters te schuiven maar door een combinatie van numerologie en een magisch vierkant.
Nadat je je intentie hebt geformuleerd, zet je de letters die je overhoudt om in cijfers. Elke letter geef je het getal waarmee het overeenkomt. Bijvoorbeeld: A = 1, B = 2, enz. ... tot aan de letter Z = 26. Je kan hier andere numerologische verbanden leggen als je dat wil (veel numerologen werken tegenwoordig met fonetische verbanden in plaats van met het alfabet), maar dat is an sich niet belangrijk. Bepaalde letters komen overeen met een getal dat uit meer dan één cijfer bestaat. Die cijfers tel je op tot je een cijfer tussen 1 en 9 overhoudt.
In de westerse numerologie wordt soms ook wel met de volgende regel gewerkt:
1 = A / J / S
2 = B / K / T
3 = C / L / U
4 = D / M / V
5 = E / N / W
6 = F / O / X
7 = G / P / Y
8 = H / Q / Z
9 = I / R
Welke vorm van numerologie je ook gebruikt – de Hebreeuwse of Griekse geomatria, de Pythogoraanse numerologie, enz. ... – is helemaal niet belangrijk, als je maar consistent bent en steeds hetzelfde systeem gebruikt.
Herinner je de intentie die we eerder formuleerden:
IK BEN EEN GEZONDE EN ENERGIEKE VROUW DIE VIJFENZESTIG KILOGRAM WEEGT
Deze intentie werd omgezet in een letterwoord:
KBNGZDRVWJFTLM
Dat letterwoord kunnen we numerologiegewijs omzetten in cijfers:
11 – 2 – 14 – 7 – 26 – 4 – 18 – 22 – 23 – 10 – 6 – 20 – 12 – 13
Verder vereenvoudigd wordt dit: 2-2-5-7-8-4-9-4-5-1-6-2-3-4
Kies vervolgens het magisch vierkant dat het beste past bij je intentie. Kijk daarvoor in de correspondentietabellen. Bijvoorbeeld: Saturnus staat voor wereldse dingen die met rijkdom te maken hebben, Venus staat voor liefdesgerelateerde intenties, enz. ... Weet je het niet zeker, gebruik dan het vierkant van Saturnus. Aangezien Saturnus verbonden is met onze materiële wereld, en we via onze runenmagie intenties willen gaan realiseren in die materiële wereld, is dat een passe-partout vierkant voor het maken van sigils.
Trek nu een lijn tussen de cijfers zodat je een symbool krijgt dat overeenkomt met je intentie. Zo heb je meteen een sigil gemaakt.
Om zelf magische vierkanten te maken, zijn er een aantal trukjes. Er is een methode voor vierkanten van een oneven orde en voor vierkanten van een even orde.
Magische vierkanten van een oneven orde:
- Teken een leeg vierkant van de orde die je wenst.
- Zet de 1 in het midden van de bovenste rij.
- Ga nu 2 hokjes naar beneden en 1 hokje naar rechts (of 1 vakje naar boven en 1 vakje naar rechts) en plaats daar het volgende cijfer.
- Als je buiten het vierkant gaat vallen aan de onderkant of de bovenkant, ga dan verder aan de onderkant of de bovenkant alsof ze als een cilinder aan elkaar zijn geplakt. Doe hetzelfde als je buiten het vierkant valt aan de rechterkant of de linkerkant, ga dan gewoon verder in de eerste kolom links of de laatste kolom rechts.
- Op een gegeven moment kom je waarschijnlijk een vakje tegen dat al gevuld is met een cijfer. Zet het volgende cijfer gewoon onder het vorige cijfer en ga verder, 2 hokjes naar beneden en 1 hokje naar rechts, enz. ...
Magische vierkanten van een even orde:
- Teken een leeg vierkant van de orde die je wenst. Teken ook de diagonalen.
- Vul het vierkant op met cijfers van 1 tot n². Voor een vierkant van orde 4 is dat van 1 tot en met 16. Begin links bovenaan en vul rij per rij het hele vierkant op.
- Spiegel nu de cijfers op de diagonalen: 1 verwissel je met 16, 6 verwissel je met 11, enz. ... Opgelet! Als het gaat om een orde van een veelvoud van 4, dan moet je niet werken met de diagonalen, maar met de subdiagonalen. Dat betekent dat je het vierkant opdeelt in vierkanten van 4 en daarvan de diagonalen spiegelt.
Vind je het te moeilijk om zelf de magische vierkanten uit te werken, dan vind je verschillende online berekeningsprograma’s op het internet die dat werkje van je overnemen (of je toelaten je eigen werk te controleren).
Werken met magische vierkanten en magische alfabetten heeft uiteindelijk tot doel om te communiceren met je onderbewustzijn (en met het collectieve onbewustzijn in de astraalwereld).
Ben je geïnteresseerd of zelfs gefascineerd door het tipje van de sluier dat hier werd opgelicht, ga dan op zoek naar informatie over de complexe methodieken van de ceremoniële magie en hoge magie. Vind je het allemaal echter veel te complex en te occult, hou het dan bij de simpele runenmagie en de correspondentietabellen. Het zou jammer zijn om het kind met het badwater weg te gooien en de hele runenmagie links te laten liggen. Deze vorm van magie is immers heel krachtig.







Reacties